因為數學不好,所以網誌成立以來一直沒有碰觸演算法相關的議題,但是隨著要分析的對象越來越複雜,可用變項指數成長,建模的時間也呈倍數縮短的情況下,還是要回到分析的根本--也就是數學模型來尋找突破的方法,所以開始認真的研讀演算法,這也是給予自己未來的目標,希望更深入的去了解常用的演算法.
不過因為數學仍然不是我的專長,所以我只能以解釋性的方式來說明對於每個算式的理解,無法太深入去推倒公式.
今天Stochastic gradient descent(簡稱SGD),Wiki上稱為梯度下降法(詳細的數學推倒課程內容可以參考Stanford ML Course,這個老師講解超級清楚!),主要是用來尋找迴歸模型的係數.當初會開始注意這個演算法,在於相較於統計上的迴歸需要一次性的將所有資料一起放入分析(又稱之為Batch Mode),SGD演算法可以單筆單筆資料放入模型中推算(又稱之為Online Mode),雖然精準度不若一次性的算法,但是卻可以即時地根據input的資料動態的調整推估model.
Batch Model和Online Model的用途以及差異其實也是和學科本身性質串在一起的.統計資料往往就是一次性的搜集然後一起分析,推算母體.但是一些物理學的資料中(SGD演算法最早提出來是在物理領域,S. Amari Natural Gradient Works Efficiently in Learning, 1988),資料(例如聲波)是不斷的發送出來的,而且還會因為環境的改變而產生變化,所以才需要這種可以動態調整的分析model.
透過回歸方程式,來看一下這種驗算法的想法以及原理(公式參考史丹佛的上課講義):
上面一條一般的回歸方程式,下面是簡化(將常數項*x0=1)(這一步其實不太重要)
先不要被公式嚇到,概念很簡單.雖然長得不一樣,但是核心原理就是最小平方法--讓預測值及觀察值的差異平方最小.θ代表了迴歸係數(單一個係數),h(x(i))為在這個迴歸係數下的預測值,y(i)為觀察值.不同的迴歸係數會得到不同的h(x(i)),我們的目的就是要尋找最合適的迴歸係數,讓這整個方程式得到最小值.
講到這裡,數學底子好的朋友應該知道我們要幹嘛了,接下來就是SGD法的概念核心--尋找最小的係數.因為時間有點晚,剩下的明天再說(待續)


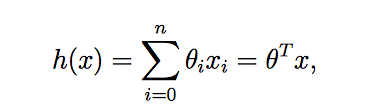

沒有留言:
張貼留言